After a brief overview of the fundamentals of graph theory and Swing, this introduction outlines the structure of the document, and the literature that was used. For additional information, updates, binaries and source code see the Home Page of JGraph at http://www.jgraph.com.
The intention of this project is to provide a freely available and fully Swing compliant implementation of a graph component. As a Swing component for graphs, JGraph is based on the mathematical theory of networks, called graph theory, and the Swing user interface library, which defines the architecture. By combining these two, a Swing user interface component to visualize graphs will be obtained. (The term graph is used in the sense of graph theory throughout this document, not to be confused with function plots.)
The following principles guided the implementation of JGraph:
Full Swing Compatibility
Clear & Efficient Design
Short Download Time
100 % Pure Java
The idea behind these principles is based on the experience with other graph libraries, which typically come as large and complex frameworks that are not standards compliant.
In JGraph instead, the basic architecture is the same as for standard Swing components, and the method and variable naming complies with Java code conventions. This has the advantage of reduced learning costs, and existing source code can be reused, resulting in shorter development time.
The concept of a graph is based on a well-founded mathematical theory, called graph theory, which is rigorously defined in [bib-Biggs], [bib-Aigner] and [bib-Ottmann]. A graph consists of vertices and of edges connecting certain pairs of vertices. The exact geometric pattern is not specified.
As a mathematical generalization of lists and trees, graphs come into play where lists and trees are not sufficient to model the relations. For example, in a tree each node has at most one parent, and zero or more children, whereas in a graph, each vertex simply has zero or more neighbors. (In the case of the list, each node has at most two neighbors.)
The single term neighbor to emphasize the more general setup replaces the terms parent and child used in the context of trees. The term cell is used in place of node throughout this document to distinguish between the elements of graphs, and those of lists and trees.
Formally, a graph G consists of a non-empty set of elements V(G) and a subset E(G) of the set of unordered pairs of distinct elements of V(G). The elements of V(G), called vertices of G, may be represented by points. If (x, y) Î E(G), then the edge (x, y) may be represented by an arc joining x and y. Then x and y are said to be adjacent, and the edge (x, y) is incident with x and y. If (x, y) is not an edge, then the vertices x and y are said to be nonadjacent.
Graph theory also offers standard algorithms to solve common graph problems. For example, the Dijkstra algorithm can be used to find the shortest path between two vertices of a graph. The Dijkstra algorithm, and many other standard algorithms are explained in [bib-Sedgewick], [bib-Nievergelt] and [bib-Harel]. (An implementation of the Dijkstra algorithm ships with the JGraphpad example application.)
To summarize, graphs are used as a paradigm in JGraph to display any network of related objects. A road or computer network, a molecule, software architecture, or database schemas are examples of graphs. Since graphs are a mathematical generalization of lists and trees, JGraph may also be used to display simpler structures, as for example a file system tree.
Swing is the user interface library that ships with Java, and provides the elements that can be placed on an application's windows. Such elements are called user interface components, or simply components. Common components are buttons, lists, trees and tables.
Swing is based on AWT, which stands for Abstract Windowing Toolkit. AWT is another user interface library that ships with Java and may be used independently of Swing. In contrast to AWT, Swing is more sophisticated, and provides many built-in features.
A good introduction to Java and AWT is given in [bib-Bishop] and [bib-Jackson]. [bib-Flanagan] and [bib-Schmid] are for the more experienced programmers. In contrast to AWT, Swing is only explained in [bib-Geary] and [bib-Geary2], and there is a good web-based Swing Tutorial [bib-Swing].
The documents mentioned before discuss existing components in great detail, but do not explain how to create new components. (Not to think of an in-depth study of Swing MVC, which is the basic architecture that all Swing components have in common [bib-GOF].) Swing's source code must be used to elaborate the required information.
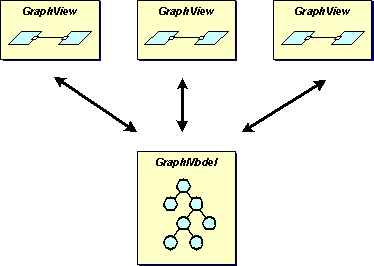
In a nutshell, the model provides the data, which is a graph ñ in the sense used in graph theory ñ and the JGraph object provides a view of the data, in platform specific manner. The Swing MVC design pattern is used to separate the model from the view and establish a relation between them, such that more than one view can be attached to the same model, and all views are automatically updated when the model changes.
JGraph is largely based on Swing's component for trees, called JTree, which is explained in [bib-JTree]. Some ideas were adopted from Swing's text components, namely the Element interface, which is discussed in [bib-Violett], and the views [bib-View]. The JGraph class itself is an extension of JComponent, which is Swing's base class for all components.
JGraph complies with all of Swing's standards, such as pluggable look & feel, datatransfer, accessibility, internationalization, and serialization. Also, all concepts used in JGraph are common, well-known concepts from Swing. For the more sophisticated features such as undo/redo, printing, and XML support, additional Swing standards were used. Aside from Swing's standards, JGraph also complies with the Java conventions for method and variable naming, source code layout, and javadoc comments.
The decomposition of JGraph into modules splits the over-all definition into a series of tractable subdefinitions. By following the MVC pattern, the framework is split into a model, view and control part. These chapters are preceded by an overview of the component.
The component overview compares JGraph to JTree, and outlines the main differences and consequences on the API. It further discusses the API with focus on the MVC pattern, and on multiple views.
The model part describes the underlying graph model interface, and selection model, and the elements that they contain; as well as the classes used to change the graph model.
The view part studies the display's internal representation of the graph, and the mapping and update between the model and the view. Special focus is given to the geometric pattern and context of graphs.
The control part explains the rendering process, the steps involved in in-place editing and cell handling, and the objects involved in datatransfer and marquee selection.
The event model is explained in an additional chapter, outlining the update and undo mechanisms, and the dynamic aspects of the system.
The final chapter summarizes the main results, draws conclusions about the current implementation, and discusses possible future enhancements.
The JGraph component is largely based on [bib-JTree]. Some ideas are used from [bib-Violett]. The description of design patterns uses the naming from [bib-GOF].
The standard book about Swing is certainly [bib-Geary] and is a good basis to understand this document. Some implementations of graph specific algorithms are based on [bib-Sedgewick] and [bib-Nievergelt]. Also, the reader should be familiar with the most important concepts of graph theory, which can be obtained from [bib-Biggs].
In addition to this paper, a tutorial [bib-Tutorial], and the API specification [bib-API] can be found on the JGraph Home Page at http://www.jgraph.com.