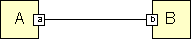The model provides the data for the graph, consisting of the cells, which may be vertices, edges or ports, and the connectivity information, which is defined using ports that make up an edge's source or target. This connectivity information is referred to as the graph structure. (The geometric pattern is not considered part of this graph structure.)
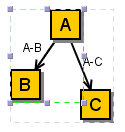
The model provides access to another structure, called the group structure. The group structure allows the cells of a graph to be nested into part-whole hierarchies, that is, it allows composing new cells out of existing ones. The following graph contains such a group, which in turn contains the vertices A and B, and the edge 1. The vertex A in turn contains the port a is a child, and the vertex B contains the ports b0 and b1 as its children.
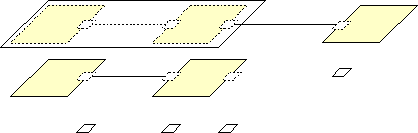
Since the group structure adds a dimension to the graph model, the above figure is not suitable to visualize both structures, even if the graph alone is fully defined. (The group in this figure is drawn using a dashed rectangle, but in reality, it is typically not visible.)
To illustrate the underlying group structure, a three-dimensional figure is used that depicts the graph structure in the X-Y-plane, and the group layers shifted along the z-axis.
The group layer diagram reveals the grouping in the graph. Dashed rectangles are used to illustrate visibility of cells on upper layers; the actual cell instances "live" on lower layers. Note that ports are part of this group structure, and appear as children of their vertices.
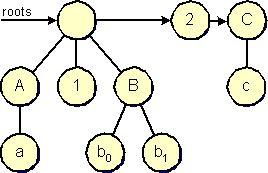
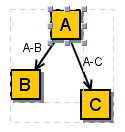
To illustrate the group structure alone, another diagram is used. In this diagram, the groups appear as trees, with their roots stored in a linked list. The elements are drawn as circles to underline the different purpose and content of the diagram. The empty cell at the root of A, 1 and B is group that has no label. It is not possible to deduce the original graph from the group structure diagram.
The group structure can be thought of as a forest of trees, where the roots of these trees may be retrieved using the GraphModel interface. Once these roots have been retrieved from the model, their descendants may be retrieved using the respective methods of the GraphModel interface.
Logically, the group structure can be seen as an extension of the TreeModel interface. However, such an extension is technically impossible because the TreeModel interface relies on TreeModelListeners, which are not used in the context of graphs.
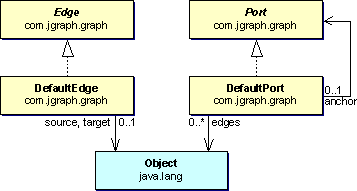
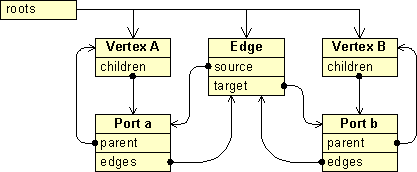
An important fact that should be kept in mind is that the source and target of an edge implement the Port interface, which is used as an indirection to provide multiple connection points for the same vertex. The relation between the port and the vertex is implemented on top of the group structure, the vertices being the parents of the ports. (Ports are somewhat artificial, and from a strictly mathematical point of view, do not belong to the definition of a graph.)
To summarize, the graph model not only provides access to the graph structure, it also provides access to an independent structure, called group structure, which allows cells to be nested into part-whole hierarchies. The group structure can be seen as a set of trees, where the roots of the trees represent the parents of the groups. (If a virtual node is added as a parent to these roots, then the model itself is a tree.) The graph structure instead provides the methods to retrieve the source and target port of an edge, and to return the edges that are connected to a port, or to an array of cells.
Graph cells are the key ingredients of JGraph, which provides default implementations for the most common cells: vertices, edges and ports. The vertex is considered as the default case, which does not need an interface, and uses the default implementation of the common superclass. Ports do not have to be treated as special children, such that their relation to the vertex can be implemented on top of the group structure, provided by the GraphModel interface.
The above only holds for the model part of the framework, the view has a different internal representation of the graph. In the view's data structure, children and ports are treated as different entities, and are kept in different lists. One of the reasons for this is that ports (if visible) do always appear in the front of the graph, regardless of their order, and the other reason is better performance.
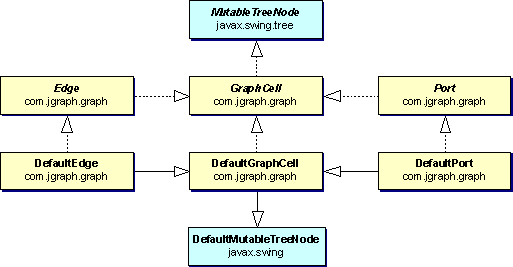
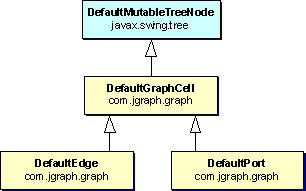
DefaultPort and DefaultEdge extend DefaultGraphCell, Port, and Edge, respectively, which in turn extend GraphCell. DefaultMutableTreeNode has a reference to a TreeNode that represents the parent, and an array of TreeNodes that represents the children. DefaultEdge has a reference to the source and target Object, which typically extend Port. DefaultPort has a reference to a Port that represents the anchor, and instantiates a set that holds the connected edges.
The GraphCell interface is an extension of Swing's MutableTreeNode interface, which provides the methods for the DefaultGraphModel to store its internal group and graph structure. The GraphCell interface itself provides methods to access the attributes of a cell, whereas the methods to access the children and parent are inherited by the MutableTreeNode interface.
The Edge interface provides the methods to access the source and target port, and the Port interface provides access to all edges attached to a specific port. Thus, the graph structure only relies on the Edge and Port interfaces.
With regard to text component analogies, the GraphCell interface is analogous to the Element interface [bib-Violett], whereas the CellView interface is JGraph's analogy to the text component's View interface [bib-View].
The abstract base class, called DefaultGraphCell, provides the functionality that is common to all graph cells, namely for
Cloning the cell and its children
Handling attributes
Synchronizing the value attribute and the user object
The DefaultGraphCell class, which is the common superclass of all graph cells, is an extension of DefaultMutableTreeNode. As a consequence, all cells in JGraph may be nested into groups.
The default implementation makes no restriction on cells being used as groups or not, and what parents and children are accepted. The programmer must ensure that only groups can be composed that make sense with respect to the application. Typically, vertices are used as groups. A vertex that is a group is invisible and only appears as a highlighted frame around its children when the group is selected.
What if a DefaultEdge is used as a group? The renderer will paint an edge between the specified source and target port, if available. A possible application is the visualization of long paths between two vertices, where the hops on the path are not important.
However, care has to be taken about the compatibility with the renderer in this case, since the renderer might rely on certain attributes to function properly. Therefore, if a cell other than a vertex is used to provide a group, it must also contain the attributes that are required by its respective renderer.
Ports may also be used as groups, which is even more "pathologic". For an explanation of the synchronization between the value attribute and the user object, please read the chapter on Attributes.
public interface GraphModel {
// Attributes
Map getAttributes(Object node);
boolean isAttributeStore();
// Roots
int getRootCount();
Object getRootAt(int index);
int getIndexOfRoot(Object root);
boolean contains(Object node);
// Layering
void toBack(Object[] cells);
void toFront(Object[] cells);
boolean isOrdered();
// Graph structure
Object getSource(Object edge);
Object getTarget(Object edge);
Iterator edges(Object port);
boolean acceptsSource(Object edge, Object port);
boolean acceptsTarget(Object edge, Object port);
// Group structure
Object getParent(Object child);
int getIndexOfChild(Object parent, Object child);
Object getChild(Object parent, int index);
int getChildCount(Object parent);
boolean isLeaf(Object node);
// Change support
void insert(Object[] roots, ConnectionSet cs, ParentMap pm, Map attributeMap);
void remove(Object[] roots);
void edit(ConnectionSet cs, Map nestedMap, ParentMap pm, UndoableEdit[] e);
// Listeners
void addGraphModelListener(GraphModelListener l);
void removeGraphModelListener(GraphModelListener l);
void addUndoableEditListener(UndoableEditListener listener);
void removeUndoableEditListener(UndoableEditListener listener);
}
The GraphModel interface defines the requirements for objects that may serve as a data source for the graph. The methods defined in this interface provide access to two independent structures:
Graph structure
Group structure
The graph structure follows the mathematical definition of a graph, where edges have a source and target, and vertices have a set of connected edges. The connection between edges and vertices is represented by a special entity, called port. In a sense, ports are children of cells and belong to the group structure. However, they are also used to describe the relations between edges and vertices, what makes them part of the graph structure.
Additionally, the GraphModel interface defines methods for the handling and registration of two different listener types: UndoableEditListeners and GraphModelListeners. The two are somewhat related in a way that every notification of the undo listener is accompanied by a notification of the model listener.
The inverse is not the case: When a change is undone or redone, the model listeners are notified in order to update the view and repaint the display, but the command history must not be updated because it already contains this specific change.
Another important feature of the GraphModel interface is the ability to decide which connections are allowed. For this purpose, the acceptsSource and acceptsTarget methods are called from the graph's UI before an edge is connected to, or disconnected from a port, with the edge and port as arguments.
By overriding these methods, a custom model can return true or false for a specific edge, port pair to indicate whether the specified connection is valid, that is, if it may be established be the graph's UI. (These methods are also called when edges are disconnected, in which case the port is null.)
It is the general practice to use the GraphModel interface to access the graph- and group structure, not the GraphCell or TreeNode interfaces that provide the same functionality. The reason for this is that the DefaultGraphModel already relies on these interfaces to implement its methods, whereas in a future implementation, a model could contain objects that do not implement the GraphCell interface, thus making it necessary for the model to store the data by other means. If the graph is accessed through the GraphModel interface, the code is independent of the model's internal structure, such that the model's implementation can be exchanged without having to change the client code.
JGraph provides a default implementation of the GraphModel interface in the form of the DefaultGraphModel class, which uses the GraphCell interface and its superclass, the MutableTreeNode interface to access the graph and group structure. This means, the model stores the data in the cells, that is, the cells make up the models group and graph data structure.
In analogy to Swing's DefaultTreeModel, which stores the data in the nodes, JGraph's DefaultGraphModel stores the data in the cells. This is efficient, but if cells are to be used in multiple models, with different relations in each model, the DefaultGraphModel is not suitable. This is because all relations are stored in the cells, making it impossible to determine the set of relations that belong to a specific model. (The same holds for the DefaultTreeModel.)
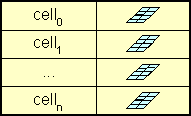
Consider for example a graph that contains two vertices A and B, and one edge. Each of the two vertices has one port as the only child, namely the port a for vertex A, and the port b for vertex B, as depicted in the figure below.
Fig. 20 shows the DefaultGraphModel's representation of the graph. The root cells, that is, the cells with a null-parent, are stored in a list and may be retrieved using the getRootCount and getRootAt methods. The children are not contained in the list, they must be accessed through the getChildCount and getChildAt methods of the model, providing the parent and, if applicable, the index of the child as an argument.
The order imposed by these methods is used as the default layering in the graph view. The layering may be changed individually for each view, thus making it possible for each view to provide its own layering.
The above figure unveils that the DefaultGraphModel contains redundancy with respect to the storage of the graph and group structure. The set of edges connected to a port is deducible from the source and target field of the edge, but requires a traversal of the graph, examining the source and target of all contained edges.
Vice versa, computing the source and target for an edge out of the ports is even more expensive, because it requires a full graph traversal and a traversal of the edge sets for each port. Because such traversal is expensive, this redundancy is used as a cache in order to improve performance when accessing the graph model.
The DefaultGraphModel implements the acceptsSource and acceptsTarget methods to return true for any arguments, and the isAttributeStore method to return false, which means that the DefaultGraphModel is not an attribute store. By extending the DefaultGraphModel, these methods may be overridden to return something more meaningful with respect to the application.
Changes to the graph model are atomic, and may be stored in a command history for later undo and redo. Possible manipulations of the graph model are:
Insert
Remove
Change
Composite changes, that is, changes that combine two or all of the above are not provided by the GraphModel interface, however, such changes are sometimes used internally, by the DefaultGraphModel.
Changes to the layering of the cells could be implemented in the model, but in JGraph's default implementation, the GraphLayoutCache class provides this functionality.
To insert and change cells, a number of classes are used as arguments to the respective methods:
Nested maps, from cells to attribute maps allow defining new or changed attributes.
The
ConnectionSetclass provides the graph structure by providing the connections to be established or removed.The
ParentMapclass describes the group structure, which consists of parent, child pairs.
The insert and edit methods allow to specify a mapping from cells to attributes. Thus, it is not only a map; it is a map of maps. This may cause confusion, especially when changing only one cell, in which case the outer map contains only one entry. In order to keep the GraphModel interface simple, however, this is the only way that individual cells may be changed, because it is the most general approach.
The ConnectionSet class is used to construct a change to the graph structure, that is, it changes the connectivity of the graph. By adding edge, port pairs, the to-be established or removed connections are defined. The name contains the term set because this object imposes a set semantic on the data that it contains.
Internally, the connections are described by instances of the Connection class, which is an inner class of the ConnectionSet class. Two connections are equal if they describe the source or target of the same edge, and the connection that is added later overrides the existing connection. (To be precise: The Connection class holds a reference to the edge, port and a boolean that indicates whether the port is a source or target. The equality is defined over the edge and the boolean.)
A connection set that describes the existing connections for an array of cells in a given model may be created using a factory method, which is a static class method that returns a ConnectionSet instance. The resulting connection set may either describe the connection, or the disconnection of the specified cells in a given model, based on a boolean argument.
The ParentMap class is used to change the group structure. Using the parent map, child, parent pairs are stored, which are then used to establish a parent-child relation between the specified cells in the model. The term map is used because this object is in fact a map, from children to parents. As with all maps, the keys are stored in a set, thus, for each child there exists exactly one parent in a parent map. Like with ConnectionSets, old entries are overridden by new entries if the same child is used twice.
Internally, the parent map counts the number of children a parent will have after its execution. A method is provided to access this count, so that future empty parents may be marked to be removed during the construction of the transaction. In this sense, there are transactions that combine the change and removal of cells, but this feature is not available through the GraphModel interface. (It is used internally, to remove groups that have no children.)
The ParentMap class provides a constructor that may be used to create the group structure for a cell array in a given model. The object may either be constructed to establish these relations, or to remove them.
When inserting cells into the model, only the topmost cell must be inserted. Since the model relies on the cell to retrieve the children, these are inserted implicitly by inserting their parent. Thus, when inserting a cell hierarchy, only the topmost cell of the hierarchy must be inserted. (While it is possible to insert the children of a cell into the model's root list, it usually should be avoided.)
Upon insertion, the model checks if it is an attribute store, and if so, it absorbs the attributes by storing them locally in the cells. (If the model is not an attribute store, then the attributes are passed to the views, and not used in the model.) An object that describes the insertion is created, executed and sent to the undo and model listeners using the model's postEdit method.
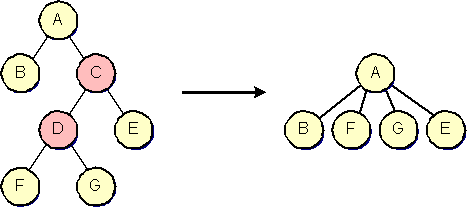
When removing cells from the model, the children must be treated in a special way, too. In contrast to the above, if children are omitted on a remove, the resulting operation is an ungroup. That is, the specified cells are removed from the root list of the model, and the first generation of children is removed from the cell, and added to the parent's parent.
Another special case is the removal of all children from a group, without removing the group (cell) itself. In this case, the default model removes the group automatically. (This also occurs when all children of a group are moved to another parent.)
On the left, the group A contains a group C, which in turn contains a group D and a cell E. The group D contains the cells F and G. In the figure on the right, the resulting group structure consists of a group A, which contains the cells B, E, F and G. The removed cells' children have been added to their parents parent, hence, they only become roots of the model if the parent was itself a root cell, that is, if its respective parent points to null.
When cells are modified, there are four arguments to the edit method: The ConnectionSet to change the graph structure, the ParentMap to change the group structure, a map of maps to change the attributes, and an array of undoable changes. The third argument is a map, from cells to attributes, which is in turn a map from keys to values. (The last argument is used internally for undo-support, by the graph view.)
If the last argument to the edit call is the only non-null argument, then the model relays the undoable changes to the undo listeners registered with it. In any other case, the model creates an object that describes the modification, executes it and notifies the undo- and model-listeners using the postEdit method.
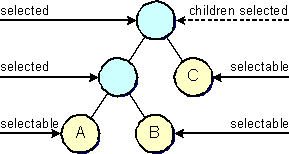
Logically, JGraph's selection model is an extension of the JTree selection model, offering all its functionality, such as single and multiple cell selection. Additionally, JGraph's selection model allows stepping into groups, as outlined below. The selection model therefore is in charge of computing the currently selectable cells based on the current selection, and it also must ensure certain properties on the selection. For example, it must ensure that a cell and its descendants are never selected at the same time.
In order to retrieve the selection candidates, that is, the cells that are currently selectable, the interface provides the getSelectables method. The stepping into feature can also be switched off, in which case the selection model offers the normal single- and multiple cell selection modes, as in the case of JTree's selection model.
When explaining the stepping into feature, it is important to outline the order in which cells are selected. The basis of this order is the view-dependent layering of the cells, or the model's order if the model is an attribute store.
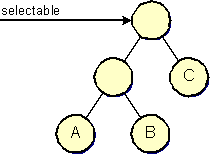
The order in which cells are selected is defined over the sequence of selectable cells, which is inductively defined by the following, and is initially equal to the model's list of root cells. (Clearly, a cell may only be selected if it is selectable, that is, if it is contained in the sequence of selectable cells.)
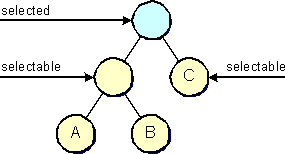
If the user clicks on the graph, the selectable sequence will be traversed, checking for each cell if it intersects the point of the mouse click. If an unselected intersecting cell is found, it will be selected, unless the isToggleSelectionEvent method returns true, in which case the topmost selected intersecting cell is removed from the selection (typically Shift-Click).
When a cell is added to the selection, its children are added between the selected cell and the next cell in the sequence (the selected cell is not removed from the sequence). Thus, the system first selects the children of the topmost cell, and then continues selecting the underlying cells, and their children respectively, upon selection of their parent.
When a cell is removed from the selection, all its children are removed from the sequence. The cell itself is deselected, but still contained in the selectable list. Thus, a cell only ever leaves the selectable list if its parent is deselected, which is only the case for non-root cells, because root cells have no parents.
Since each view may provide a different layering for the cells, and the selection model has no notion of view-layering, the selectable list that the selection model returns is more precisely defined as a set of candidates to be selected. The set is then turned in to a sequence by ordering the cells based on the view-dependent layering according to the rules stated above.